Vistas Gráficas.
La introducción de una segunda ventana gráfica aumenta las chances de comprobar / comparar construcciones similares desde diferentes perspectivas. Un ejemplo práctico de la conveniencia de estas dos vistas podría ser la consideración por separado de una función y su derivada o, simplemente, incluir el texto de una descripción o planteo en una de las ventanas. El mapa de una vista del trazado se realiza o puede ser reajustada en el Cuadro de Propiedades del objeto.
- → Ejercicio: trazado gráfico de la función derivada y empleo de la otra vista para establecer inferencias.
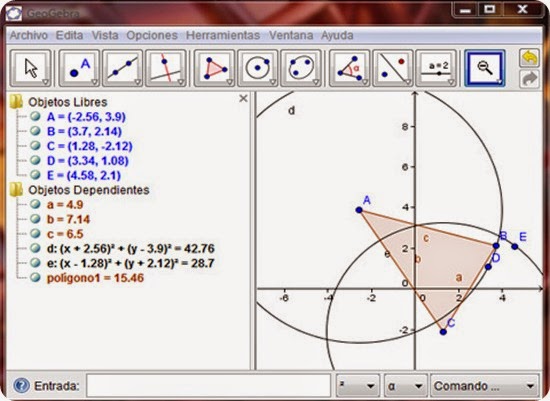
- → Ejercicio: representación de la circunferencia trigonométrica unitaria y las funciones trigonométricas dependientes del ángulo.
Incluso respecto de los caracteres asociados, por ejemplo, a los ejes, se pueden tomar decisiones en relación a las vistas para establecer alternativas de distinción de los ejes. De este modo se pueden limitar los ejes como para representar exclusivamente los valores positivos o siempre sobre el borde de los ejes. Además, se pueden se pueden trazar funciones cuya variable independiente no sea necesariamente x. A la alternativa existente de indicar en coordenadas polares la ubicación de un punto, se suma la de emplear la cuadrícula de tales coordenadas que ahora está disponible.
Vista Algebraica.
Una no por pequeña menos valiosa mejora en la Vista Algebraica es la exposición de los objetos usando LaTeX.
Incluso, se ven correctamente en esta vista, vectores y matrices.
Novedades para uso de Pizarras Digitales y otros dispositivos de contacto.
Como crear un applet suele requerir de teclado, debían emplearse trucos diversos para lograrlo sobre una pizarra digital. Ahora este tipo de maniobras se ha simplificado por contar con novedosos recursos.
- La mencionada barra de estilo permite un acceso más veloz a las propiedades de los objetos. Esto agiliza lo que antes requería de la incómoda operación dentro del Cuadro de Propiedades.
- Además de poder guardar las propiedades, también se pueden almacenar las preferencias asociadas a los objetos. Entre los ajustes ahora hay una lista de todos los objetos donde se pueden establecer los estilos y rasgos en que se prefiere cada uno de los comprendidos.
- Un teclado virtual, que aparece con un clic sobre el correspondiente campo de entrada (una vez que se lo haya habilitado).
- Para los alumnos de nivel primario o para quienes tengan dificultad de alcanzar la zona superior de la pantalla, ahora se puede ubicar la barra de 'Herramientas en la franja inferior.
- Para hacer anotaciones o esbozos sobre una construcción, se puede emplear la Herramienta Lápiz'. Así, la imagen resultante puede almacenarse tal como resulte en la Vista Gráfica de GeoGebra.
Nota:
Se pueden probar las versiones en desarrollo de GeoGebra para teléfonos móviles. Si se cuenta con un dispositivo con capacidad para buscadores con alcance de JavaScript se lo puede probar visitando GeoGebraTube.
Previamente debe fijarse el dispositivo como "móvil" y luego acudir al servidor GeoGebraTube de modo que se cuente con respaldo de Java. Esta alternativa no es funcional para cualquier boceto. Por ejemplo, no lo es con bocetos que incluyen guiones.
Si te ha gustado el artículo inscribete al feed clicando en la imagen más abajo para tenerte siempre actualizado sobre los nuevos contenidos del blog: 











0 comentarios:
Publicar un comentario
No insertes enlaces clicables, de lo contrario se eliminará el comentario. Si quieres ser advertido via email de los nuevos comentarios marca la casilla "Avisarme". Si te ayudé con la publicación o con las respuestas a los comentarios, compártelo en Facebook,Twitter o Instagram. Gracias.